The Broken Bay Software Co.
0%

Enabling Constraints

نُشر في

Enabling Constraints

I’ve been playing around with “constraint mapping” as part of a crowdsourcing thing Cognitive Edge did earlier this year. They are moving to different terminolgy now and already have methods. I first did this with Civilian Applications as part of my research project with UTS but I thought I’d share the full method here and keep this post updated as I improve on it.

Enabling Constraints

Materials/resources

  • Whiteboard OR paper on a table ( or digital equivalent like Miro.com)
  • Sticky-notes
  • Black sharpies
  • Coloured whiteboard markers, crayons etc
  • The matrix typology of constraints (printout, URL, on the Miro board etc.)

Preparation

  1. Introduce the idea that we’re here to make a “flower”. Have some examples of colourful finished flowers from previous sessions but with the words blurred out

  2. Clearly state what we’re here to work on or make sense of - eg. “our company”, “this team”, “the current pandemic in Australia”, “the new product we want to make”

  3. If < 6 people, make one group. If there’s > 6 people, break into groups of 3 - 4 people. If possible, put people who work together or know each other well in the same group - e.g. a group of managers, a group of designers, a group of friends. The idea is to encourage group convergence

  4. Start with a blank slate and introduce the idea of the full entropy/chaotic state where all things are equally possible and nothing can happen

  5. Introduce the idea of enabling constraints

  6. Go through the typology of constraints with examples. Discussion and questions are good so ask questions if there aren’t any coming in - NOTE: The Cynefin typology is depricated so I might use my own at some point

Workflow

Containers:

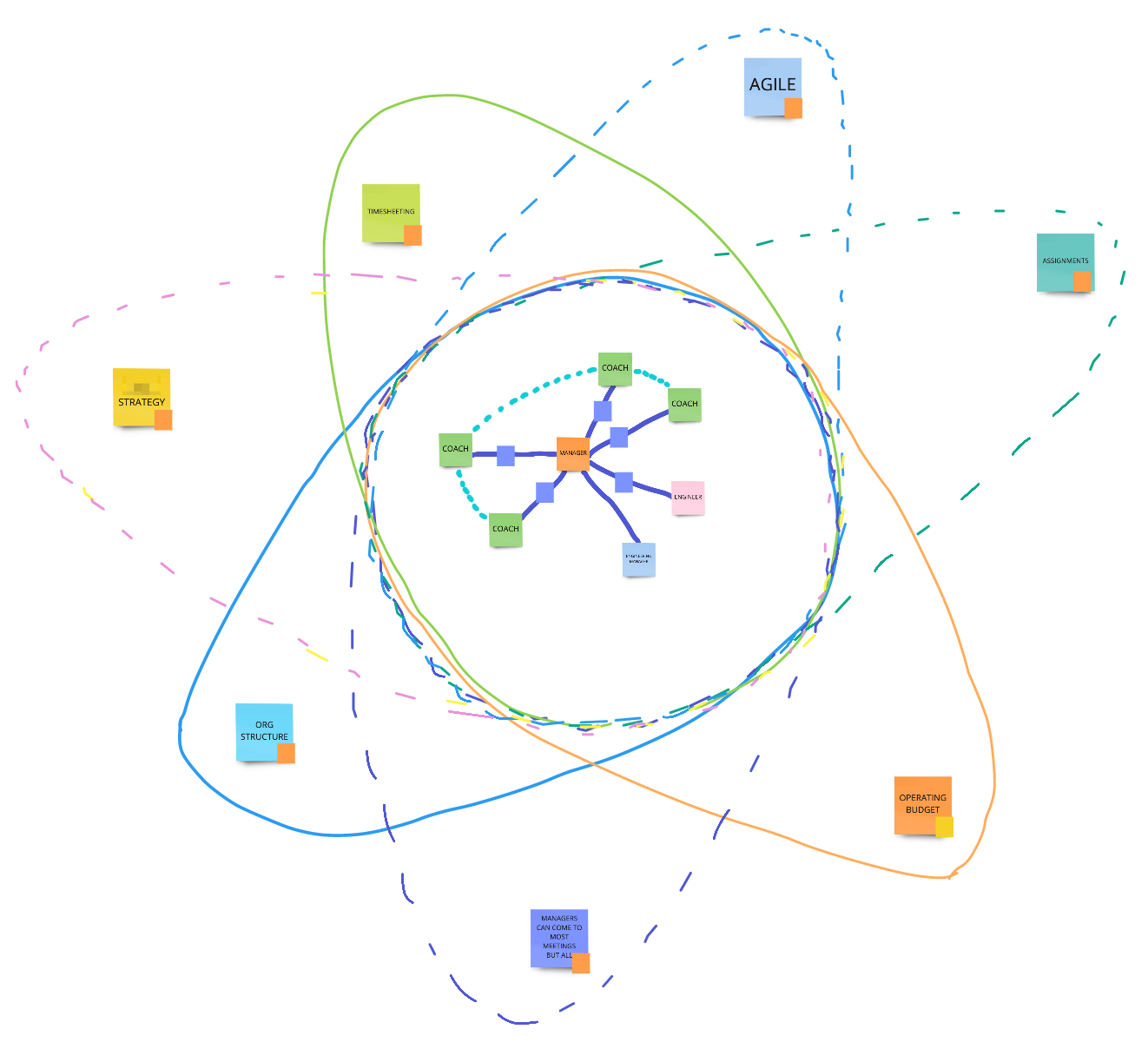
  1. Invite each group to draw a dotted-line circle in the middle of their blank field with a diameter about half the smallest dimension of the field. Say, “ok, that’s ——————“ (whatever situation we’re here to work on).

  2. Invite them to consider what Rigid/Fixed constraint is making this situation happen or will make it possible (if it hasn’t happened yet). Demonstrate drawing a teardrop shape around the situation with a sticky-note label in the pointy end of the teardrop. The sticky should say the name of the constraint and “Rigid/Fixed” as well. Explain that an unbroken line means it’s a “Robust” constraint, and that a broken line will mean it’s a “Resilient” constraint when we get to those.

  3. Give a time-box of 20 minutes and ask the groups to go through each type of container from left to right in the table. When they find one example, draw and label it, then ask if there are any more of the same type. If there isn’t, move on to the next type and pick a new colour for it.

  4. You can walk around and help people if they need to clarify the procedure. Resist the urge to suggest examples.

Connections:

  1. After the time-box is up, demonstrate putting two stickies inside the container. Give them generic labels like “person” and “thing”. Connect the two stickies with a solid line to show a Robust/Fixed connection. Remind them, that a solid line means “Rigid/Fixed” and a broken line means “Resilient”

  2. Set a timebox of 3 minutes and ask the groups work as individuals and generate stickies for all the different kinds of people and things that might be inside the system. Ask them not to use names.

  3. Set a timebox of 5 minutes and ask them to share and consolidate their stickies, removing duplicates

  4. Set a timebox of 20 minutes and ask the groups to go through each type of connection from left to right in the table. When they find one example of the type of connection, draw and label it with a sticky (only one sticky is needed for each type because they’ll all be the same colour). Ask if there are any more of the same type. If there isn’t, move on to the next type and pick a new colour for it.

  5. You can walk around and help people if they need to clarify the procedure. Resist the urge to suggest examples.

Debrief

  • If there is more than one group, get them to rotate around looking at each other’s “constraint flower”. Each time they rotate ask them to note down one thing that is the same, one thing that is different and one thing that is surprising about this group’s flower compared to their own. When every group has seen every other group’s flower, invite them to share their notes
  • If there is only one group, invite them to silently write down, on a sticky, at least one thing they learned while making the flower. Invite each person to put their sticky around the flower, saying that they learned as they do so.